最終更新日:
【スペクトル解析】音声信号処理の基礎知識シリーズその2

こんにちは。スキルアップAIの小宮です。本ブログでは、AI を用いた音声・音楽モデルに必要な、音声信号処理の基礎知識について解説します。第2回の今回は、スペクトル解析について解説します。
第1回の内容はこちらです。
1.スペクトル解析
音声データの分析においては、音声波形そのものを分析するということは少なく、通常は周波数成分に分解した状態で分析を行います。フーリエ変換を用いて音声波形を周波数成分に分解したものをスペクトル(Spectrum)と呼び、スペクトルを解析することをスペクトル解析と呼びます。
1-1.フーリエ変換
音声波形を周波数成分に分解する際にはフーリエ変換を用います。コンピュータで扱われる音声信号は離散信号(デジタル信号)であるため、フーリエ変換の中でも離散フーリエ変換を用います。元の音声信号を x 、スペクトルを X とおくと離散フーリエ変換は次のように定式化されます。
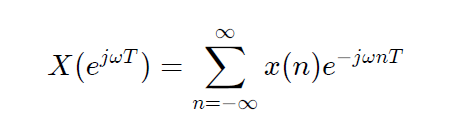
x(n) は元の音声信号のn番目の値、T はサンプリング周期(サンプリング周波数の逆数)であり、nT は 1 サンプルあたりの時間を表しています。 一見すると複雑ですが、この式は波形に関する公式(①)とオイラーの公式(②)の知識があれば理解することができます。
①周波数 f・角速度 ω・角度 θ・時間 t の関係式波形に関する公式
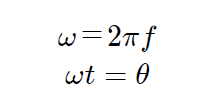
②複素指数関数と三角関数の間の関係式(オイラーの公式)
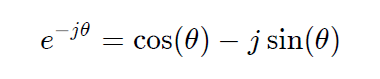
この2式を踏まえると、最初のフーリエ変換の式は「ある角速度 ω における周波数成分は、信号のサンプルに角速度 ω のコサイン波・サイン波を掛け合わせたものを、全サンプル分足し合わせることにより求められる」ということを表しているといえます。
1-2.スペクトルとスペクトログラム
フーリエ変換の結果は実部(コサイン波)と虚部(サイン波)の複素数となり、その絶対値を取るとスペクトルを見ることができます。 スペクトルを時間方向に並べたものを、スペクトログラム(Spectrogram)またはソナグラム(Sonagram)と呼びます。スペクトルは2次元(周波数×振幅)、スペクトログラムは3次元(周波数×時間×振幅)のデータです。
1-3.FFT(高速フーリエ変換)
スペクトルを算出するための数値計算ライブラリでは、高速フーリエ変換(FFT: Fast Fourier Transform)という手法が用いられています。また、音声波形を短い区間に切り分け、窓関数を掛けながら FFTを実行することを短時間フーリエ解析といいます。短時間フーリエ解析を行うとソナグラムが出力されます。
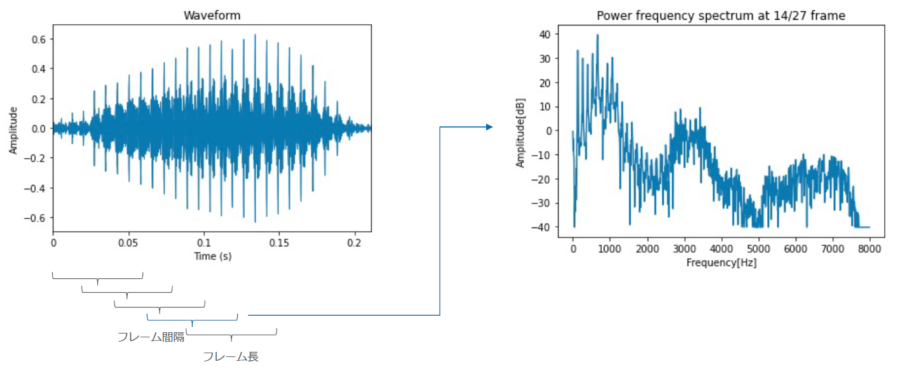
図1. 音声波形とスペクトルの例
短時間フーリエ解析を行うための関数では、通常、n_fft(フレーム長)・hop_length(フレーム間隔)・win_length(窓関数の長さ)の3つの引数を受け取ります。
n_fft は切り出す区間の長さ、win_length は切り出した波形に掛ける窓関数の長さを表します。基本的には同じ値を用いますが、win_length を n_fft より小さく設定すると、波形の特徴を強調することができます。また hop_length は、波形を切り出す間隔を表します。これを小さくすると、出力されるソナグラムが時間方向に長くなります。
n_fft や win_length を大きくすると周波数分解能が細かくなりますが、時間分解能は粗くなってしまいます。逆に時間分解能が細かすぎると、低い音(波長の長い信号)を捉えることができません。低い音を解析するためには、その波形を少なくとも3波含むようにパラメータを設定する必要があります。
2.スペクトルから派生した特徴量
音声認識・音声合成のモデルでは、入力データとして、スペクトルから取り出した情報がよく用いられます。
2-1.ケプストラム
対数スペクトルを波形とみなしてフーリエ変換したものをケプストラム(Cepstrum)と呼びます。また、ケプストラムの横軸をケフレンシー(Quefrency)と呼びます。ケフレンシーの低い部分を取り出して逆フーリエ変換を行うと、スペクトル包絡(声道の特性を表す特徴量)を取り出すことができます。
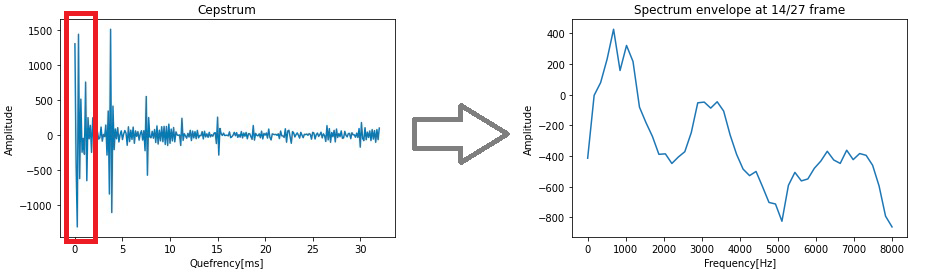
図2:ケプストラムとスペクトル包絡の例
2-2.メルスペクトル
人間の聴覚には、高い音ほど音高(音の高さ)の変化に鈍感になるという特性があります。その知覚特性を考慮した尺度をメル尺度と呼びます。メル尺度における数値の差は、人間が感じる音高の差とほぼ同じになっています。また、スペクトルの周波数をメル尺度に変換したものをメルスペクトルと呼びます。
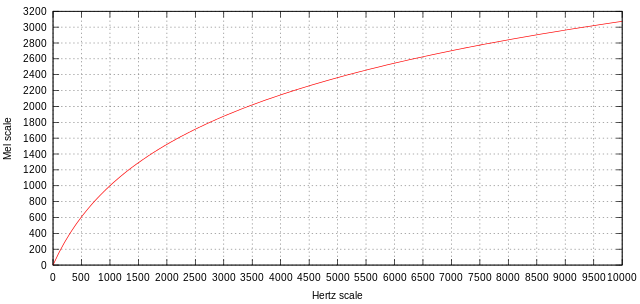
図3:周波数[Hz]とメル尺度 (基準周波数 700 Hz) の関係
2-3.MFCC
メルスペクトルからケプストラムを算出し、さらに対数をとったあとに、離散コサイン変換を行ったものを MFCC(メル周波数ケプストラム係数)と呼びます。MFCC の低い方から 12~18 次元ほどを取り出したものは、スペクトル包絡のような声道特性(話者の特徴)を表します。
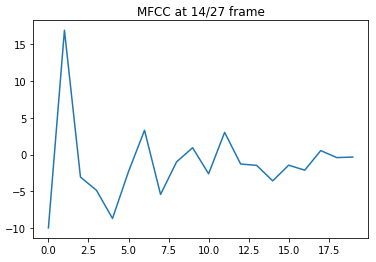
図4:MFCCの例
3.まとめ
今回は、波形をスペクトルに変換するためのフーリエ変換と、スペクトルから派生した特徴量を紹介しました。データサイズの関係上、従来はMFCCが多く用いられていましたが、ディープラーニングの登場以降はメルスペクトルを用いることが主流です。
次回は、音声認識システムの概要について解説します。
4.おわりに
プログラミング言語の1つであるPythonを用いると、音声をはじめとした様々なデータを手軽に扱うことができます。スペクトル解析を行うには、Python用の音声処理ライブラリの1つであるLibrosaを用いると便利です。
スキルアップAIでは、「機械学習のためのPython入門講座」を開講中です。本講座では、Pythonの基本的な使い方から、scikit-learnを用いた機械学習モデルの構築までを学ぶことができます。 ぜひ受講をご検討ください。
また、毎週水曜日に実践的AI勉強会「スキルアップAIキャンプ」を開催しています。勉強会では、様々な実践的テーマを取り上げ、データ分析・AI開発の実務力アップにつながるヒントをご提供します。講師が参加者の皆さんからの質問や悩みに答えるコーナーもあります。
興味がある方はぜひ参加してみてください!
第1回「音データのしくみ」はこちら
音声信号処理の基礎知識シリーズの記事一覧はこちら
5.参考文献

【監修】スキルアップAI 取締役CTO 小縣信也
AI指導実績は国内トップクラス。「太陽光発電発電量予測および異常検知」など、多数のAI開発案件を手掛けている。日本ディープラーニング協会主催2018E資格試験 優秀賞受賞、2019#1E資格試験優秀賞受賞。著書「徹底攻略ディープラーニングE資格エンジニア問題集」(インプレス)。
配信を希望される方はこちら
また、SNSでも様々なコンテンツをお届けしています。興味を持った方は是非チェックしてください♪
公開日: